একটি স্কুলের ম্যানেজিং কমিটি তাদের স্কুলের 10 জন গরীব শিক্ষার্থীর জন্য দুঃস্থ কল্যাণ তহবিল থেকে a টাকা বরাদ্দ করল। সেই টাকা থেকে প্রত্যেক শিক্ষার্থীকে প্রতিটি b টাকা মূল্যের 2 টি করে খাতা ও প্রতিটি c টাকা মূল্যের 1টি করে কলম বিতরণ করা হলো। এতে কিছু টাকা উদ্বৃত্ত হলো। এই টাকার সাথে আরও d টাকা যোগ করে তা 2 জন প্রতিবন্ধী শিক্ষার্থীর মধ্যে সমানভাবে ভাগ করে দেওয়া হলো।
উপরে বর্ণিত তথ্যগুলোকে বীজগণিতীয় রাশির মাধ্যমে প্রকাশ করতে পারি:
]
এখানে, ১ম বন্ধনী (), ২য় বন্ধনী {}, ৩য় বন্ধনী [] ব্যবহার করা হয়েছে। বন্ধনী স্থাপনের নিয়ম হচ্ছে [[()]]। এ ছাড়াও রাশিটিতে প্রক্রিয়া চিহ্ন,, ও ব্যবহার করা হয়েছে। এরূপ রাশির সরলীকরণে 'BEDMAS' (B for Braket, E for Exponent, D for Division, M for Multiplication, A for Addition. S for Subtraction) অনুসরণ করা হয়। আবার, বন্ধনীর ক্ষেত্রে পর্যায়ক্রমে ১ম, ২য় ও ৩য় বন্ধনীর কাজ করতে হয়।
বন্ধনী অপসারণ:
লক্ষ করি: b > c
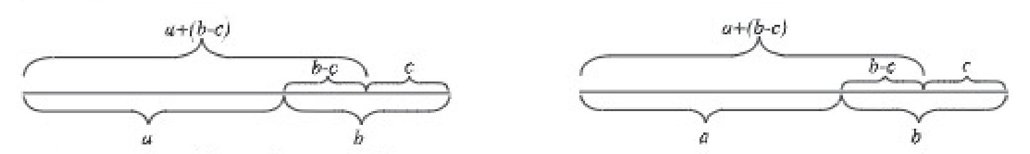
চিত্রে দেখা যায়, a + (b - c) = a + b - c
| বন্ধনীর আগে '+' চিহ্ন থাকলে, বন্ধনী অপসারণে বন্ধনীর ভিতরের পদগুলোর চিহ্নের পরিবর্তন হয় না। |
আবার, লক্ষ করি: b > c a > b - c
চিত্রে দেখা যায়, a - (b - c) = a - b + c
লক্ষ করি: a - (b - c) + (b - c) = a
আবার, a - b + c + (b - c) = a
সুতরাং, a - (b - c) = a - b + c
[ - (b - c) এর যোগাত্মক বিপরীত (b - c) ]
| বন্ধনীর আগে'-' চিহ্ন থাকলে, বন্ধনী অপসারণে বন্ধনীর ভিতরের পদগুলোর চিহ্নের পরিবর্তন হয়ে বিপরীত চিহ্নযুক্ত হয়। |
| কাজ: নিচের রাশিগুলোর বন্ধনী অপসারণ কর। | |
| বন্ধনীযুক্ত রাশি | বন্ধনীমুক্ত রাশি |
| 8+(6-2) | |
| 8-(6-2) | 8-6+2 |
| p+q+(r-s) | |
| p+q-(r-s) | |
| কাজ: নিচের রাশিগুলোর মান অপরিবর্তিত রেখে বন্ধনী স্থাপন কর। | |||
| রাশি | বন্ধনীর আগের চিহ্ন | বন্ধনীর অবস্থান | বন্ধনীযুক্ত রাশি |
| 7+5-2 | + | ২য় ও ৩য় পদ ১ম বন্ধনীভুক্ত অর্থাৎ, (5-2) | 7+(5-2) |
| 7-5+2 | - | ২য় ও ৩য় পদ ১ম বন্ধনীভুক্ত অর্থাৎ (-5 + 2) | 7-(5-2) |
| a-b+c-d | + | ৩য় ও ৪র্থ পদ ১ম বন্ধনীভুক্ত | |
| a-b-c-d | - | ||
উদাহরণ ২১। সরল কর 6 - 2{5 - (8 - 3) + (5 + 2)}
সমাধান:
6 - 2{5 - (8 - 3) + (5 + 2)}
= 6 - 2{5 - 5 + 7}
= 6 - 2{7}
=6-14
=-8
উদাহরণ ২২। সরল কর: a+ b - (c - d)
সমাধান:
a + {b - (c - d)}
= a + {b - c + d}
= a + b - c + d
উদাহরণ ২৩। সরল কর: a - [b - {c - (d - e)} - f]
সমাধান:
a - [b - {c - (d - e)} - f]
= a - [b - {c - d + e} - f]
= a - [b - c + d - e - f]
= a - b + c - d + e + f
উদাহরণ ২৪। সরল কর 3x - [5y - {10z - (5x - 10y + 3z)}]
সমাধান:
3x - [5y - {10z - (5x - 10y + 3z)}]
= 3x - [5y - {10z - 5x + 10y - 3z}]
= 3x - [5y - {7z - 5x + 10y}]
= 3x - [5y - 7z + 5x - 10y]
= 3x - [5x - 5y - 7z]
= 3x - 5x + 5y + 7z
= - 2x + 5y + 7z
= 5y - 2x + 7z
উদাহরণ ২৫। 3x - 4y - 8z + 5 এর তৃতীয় ও চতুর্থ পদ বন্ধনীর আগে (-) চিহ্ন দিয়ে প্রথম বন্ধনীভুক্ত কর। পরবর্তীতে দ্বিতীয় পদ ও প্রথম বন্ধনীভুক্ত রাশিকে দ্বিতীয় বন্ধনীভুক্ত কর যেন বন্ধনীর আগে (-) চিহ্ন থাকে।
সমাধান:
3x - 4y - 8z + 5 রাশিটির তৃতীয় ও চতুর্থ পদ যথাক্রমে ৪৫ ও 5 প্রশ্নানুসারে, 3x - 4y - (8z - 5) আবার, 3x - {4y + (8z - 5)}
কাজ: সরল কর: 1 . x - {2x - (3y - 4x + 2y)} 2 . 8x + y - [7x - {5x - (4x - 3x - y) + 2y}] |
common.read_more
common.or
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
Lorem ipsum dolor, sit amet consectetur adipisicing elit. Ducimus nihil, quo, quis minus aspernatur expedita, incidunt facilis aliquid inventore voluptate dolores accusantium laborum labore a dolorum dolore omnis qui? Consequuntur sed facilis repellendus corrupti amet in quibusdam ducimus illo autem, a praesentium.
1 hour ago
